This tutorial introduces the topic of microstructure characterization by means of peak broadening analysis, in the hypothesis of isotropic size and strain effects. For a thorough review of microstructure analysis through X-Ray diffraction see e.g. https://doi.org/10.1007/978-3-662-06723-9. ReX currently implements two models for isotropic size/strain analysis which will be shortly described and applied to powder diffraction data collected during the Size/Strain round-robin carried out on a CeO2 sample.
To begin the tutorial, make sure you have downloaded and extracted the archive containing the examples data. The size_strain folder contains the calibration project file as well as the experimental data. After starting ReX, load the calibration file size_strain.rxp by selecting the “Load project” button 
in the main toolbar or the corresponding main menu item. The calibration contains the instrumental parameters refined against the lebailsh.xy file relative to the annealed Ceria sample (included for reference only; see here for a tutorial on on how to perform instrument calibration with ReX). Next, load the lebailbr.xy data file relative to the as-synthesized Ceria sample by selecting the Dataset node in the project tree and choosing the “load data” command 
from the main toolbar (or the corresponding context menu), or simply dragging and dropping the file over the Dataset node in the project tree. Choose “Add to current dataset” when prompted; the pattern will be added to the selected dataset and displayed in the Dataset plot window. As usual, you may want to select the “square root” option in the Y scale command 
in the window menu to better visualize high-angle peaks.
Now, we need to load the CeO2 crystallographic information file file from the database; to do so, select the “Sample” node in the project tree and select the “Load Object” command from the menu in the main toolbar. Load the CeO2.cif file from the example folder; after a confirmation dialog, the phase should appear as a sub-node of Sample in the project tree. Press the “Update default analysis” 
button on the main toolbar to update the model; in the Dataset plot window, the modeled powder diffraction pattern should appear superimposed to the observed one:
Calculated Bragg peak positions are reasonably correct whereas background and, most importantly, modeled peak shapes are far different from the observed ones. To perform a first preliminary refinement, go to the parameters tree view, and enable the scale factor and background parameters by checking the corresponding checkboxes:
Click the “Run default analysis” 
button in the main toolbar to start the refinement, which should complete in a few iterations giving a better background fit:
A small mismatch between experimental and calculated peak positions is observable, possibly due to sample misalignment and / or a CeO2 lattice parameter slightly different from the literature reference; in this case, it is safe to refine both parameters at the same time, since they are not correlated between each other. To do so, enable the corresponding check-boxes in the Instrument and Cerium Oxide parameter sub-trees, after selecting the corresponding nodes in the Project tree:
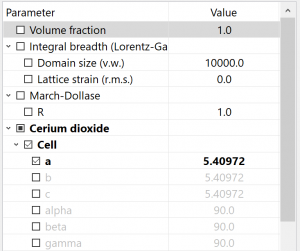
The refinement should result in a slightly improved Rwp value. After that, we can start with the actual microstructural analysis of the CeO2 phase. Select the Cerium Oxide phase in the project tree; in the corresponding properties panel, the “Integral Breadth ( Lorentz/Gauss)” model should be enabled by default in the Size-strain broadening combo box.
This simple model assumes a pure Lorentzian contribution for size broadening and pure Gaussian contribution for strain broadening. The advantage of this model is that average volume-weighted crystallite size and max root-mean-square strain are included as directly refinable parameters. Of course, values obtained with this model should be considered for a semi-quantitative evaluation at best. In the parameter tree, check the “Domain size” checkbox; to help the refinement converge faster, you may want to put a more sensible starting value than the default one (e.g. 500 Å):
After running the refinement, a value around 240 Å should be obtained for the average, volume weighted domain size. Enabling also the parameter relative to the average lattice strain in the refinement should result in a very small value of the r.m.s. strain, with a negligible change in the domain size; this can hint at a size-dominant broadening effect.
A better approximation in terms of the physical description of size/strain broadening phenomena can be obtained by means of the so-called Double-Voigt model, which can be assumed as consistently related to the Warren-Averbach approximation. In this case, size and strain broadening effects are modeled by means of two different Voigt functions, so that in general they can have both a Gaussian and Lorentzian component. From a refinement perspective, optimizable parameters are indeed the Lorentzian an Gaussian components of the integral breadths (IB) the two Voigt functions, for a total of our parameters; average volume and area weighted crystallite sizes, as well as maximum strains are then calculated from the refined I.B. values as described in great details here.
To proceed, select the Cerium Oxide node in the project tree and then choose the “Double-Voigt (Isotropic)” model in the size/strain broadening combo-box:
In the Parameter sub-tree of the Cerium Oxide phase, the four parameters corresponding to the Gaussian and Lorentzian components of the two Voigt functions describing size and strain broadening are visible, expressed in radians * 1E-3 (a 1E-4 radians value should be set by default for all parameters). Since – from the previous analysis – we expect that most of the peak broadening is coming from size effects, we are going to refine the two size related parameters first (e.g. Beta size (Gauss) and Beta size (Lorentz)):
The refinement should converge to intermediate values of about 2.3*10-3 and 2.5*10-3 radians for the Gaussian and Lorentzian size components, respectively. In the following refinement, we can also enable the strain related coefficients (Beta strain (Gauss) and Beta strain (Lorentz)) which should converge to values slightly higher than zero; this also should result in a minor change of the size related coefficients:
In the properties panel of the “Double Voigt (Isotropic)” model the size and strain quantities calculated from the refined coefficients are reported, in particular the Area and Volume Weighted average domain sizes expressed in Angstroms, Da and Dv, as well as the maximum strains calculated for Da/2 and Dv/2, Eps(Da/2) and Eps(Dv/2):
Given the model complexity, it is possible to obtain slightly different values of size and strain coefficients (and the derived quantities) depending on the refinement order and starting parameter values. Checking the high angle region of the pattern, we can also observe a small mismatch between experimental and calculated peak shapes, likely due to an imperfect modeling of integrated peak intensities:
As a possible solution and further exercise, it is suggested to try and refine the isotropic displacement factors of Ce and O atom in the Cerium Oxide structure, and check the possible effect this can have on the variation on the size/strain model parameters.